| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- nan값
- 강의정리
- 에스토스테네스의 체
- 파이썬 머신러닝 완벽가이드 공부
- 질문 정리
- 수학
- numpy
- CS224W
- BruteForceSearch
- allow_pickle
- 백준
- 소수 판정
- graph
- 유클리드 호제법
- Graph Representation Learning
- paper review
- #나동빈
- 논문리뷰
- 이코테
- BruteForchSearch
- #이코테2021
- 데이콘 필사
- 추천시스템 입문
- zerodivide
- 추천시스템
- 나동빈
- 알고리즘
- 코테공부
- 그래프란
- 글또8기
- Today
- Total
꾸준히 써보는 공부 기록
CS224W(2021) Lec 2-2 정리 본문
참고자료: Hamilton-Graph Representation Learning, CS224W Lecture Note
3. Link Prediction Task and Features
Link-Level Prediction Task as Task
존재하는 link들을 기반으로 새로운 link를 예측하는 task이다.
Test를 할 때, 모든 노드 pair들의 Rank를 매긴다. (존재하는 link는 제외한다.)
그리고 Rank가 높은 top $K$ node pair들을 예측한다.
이 때 핵심은, node들의 pair의 feature들을 design하는 것이다.

Link prediction은 두 가지 formulation들로 나타낼 수 있다.
Two formulations of the link prediction task
1) Links missing at random
random하게 link들을 지우고 그 지웠던 link를 예측한다.
2) Links over time
주어진 $G[t_0, t_0']$ (time $t_0'$ 까지의 edge들로 구성된 graph) 에 대해서,
다른 time의 graph인 $G[t_1, t_1']$에서 나타날 것이라고 예측되는 link들에 대해서 ranking을 매긴
Ranked List $L$을 output으로 내보낸다.
Evaluation
$n=|E_{new}|$ : test period $[t_1, t_1']$ 동안 나타나는 새로운 edge들의 개수
$L$에서 top $n$ element를 가져오고 여기서 맞은 edge의 개수를 count !!

Link Prediction via Proximity
Methodology
각 node pair $(x,y)$에 대해서, score $c(x,y)$를 계산한다.
예를 들면 score는 x와 y의 공통된 이웃들의 수라고 할 수 있다.
⇒ pairs $(x,y)$를 score를 기반으로 sort한다.
⇒ 새로운 link로써 top $n$ pair들을 예측한다.

1) Distance-Based Features
두 노드들 사이의 Shortest-path의 Distance !!

하지만, 이 경우 neighborhood overlap의 degree를 찾아내지 못한다.
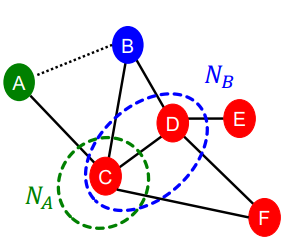
Node pair (B, H) 는 2개의 node를 share하고 있는데, pair (B, E)와 (A, B)는 1개의 node를 share한다.
구체적으로 세분화가 어렵다..
2) Local Neighborhood Overlap
두 개의 node $v_1$와 $v_2$ 사이에서 share된 neighboring node들의 개수를 찾는다
Common neighbors : $|N(v_1) \cap N(v_2)|$
(공통으로 인접한 node)
Jaccard's coefficient : $\frac{| N(v_1) \cap N(v_2)|}{| N(v_1) \cup N(v_2)|}$
(common neighbors의 normalized version)
Adamic-Adar index: : $\sum_{u \in N(v_1) \cap N_(v_2)} \frac{1}{log(k_u)}$
(실제로 많이 사용되는 형태로, social network에서 잘 동작한다고 한다.)
(node v1과 v2가 공통으로 가지는 이웃들에 대해서 sum)
3) Global Neighborhood Overlap
Local neighborhood features의 limitation은
공통되는 이웃이 없을 때 metric은 항상 0이 된다.

Global neighborhood overlap metric은 전체 graph를 고려하게 되면서
이러한 한계점을 해결해주게 된다.
Q: How to compute #paths between two nodes?
A: graph adjacency matrix의 power를 사용하는 것이다.
이것의 의미는???
- $P_{12}^{(1)}$는 node 1과 node 2사이의 직접적으로 연결된 이웃들의 path 개수를 의미 (1 hop !!)

$P_{uv}^{(2)}$는 2 hop을 의미하게 된다!! 그러니깐 한 다리 더 건너 있는 이웃을 의미함!!
(neighbor of neighbor) ⇒ (length 2)

Katz index between $v_1$ and $v_2$
노드 pair들 사이에 모든 길이의 path들의 개수를 세는 것이다 !!

위의 식을 다시 closed-form으로 연산을 하면 다음과 같이 된다.
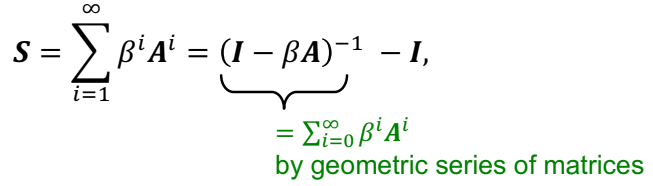
4. Graph-Level Features and Graph Kernels
Graph-Level Features
전체 graph의 구조를 나타내는 feature를 학습시키는 것이 목표이다 !!
Background : Kernel Methods
Kernel method들은 graph-level prediction을 할 때 전통적인 ML에서 사용되던 방법이다.
Idea: feature vector들 대신 kernel들을 디자인
Kernel이란 ??
Kernel $K(G,G') \in \mathbb{R}$은 similarity를 측정한다.
Kernel matrix $K=(K(G,G'))_{G,G'}$은 항상 양수가 된다. (positive semidefinite)
Feature representation : $\phi(\cdot)$
$K(G,G')=\phi(G)^T\phi(G')$
Kernel이 정의되면,
(Kernel SVM과 같은) off-the-shelf ML model은 prediction을 하는데 사용할 수 있다.
Graph-Level Features: Overview
Graph Kernels
두 그래프 사이의 similarity를 측정하게 된다.
1) Graphlet Kernel
2) Weisfeiler-Lehman Kernel
여기서는 이 2가지 방법만 소개한다고 한다 !!
Goal : graph feature vector $\phi(G)$를 디자인
Key idea : graph를 위한 Bag-of-Words (BoW)
BoW는 단순하게 document들의 feature값으로 word count 값을 사용하는 것이다.
node들을 단어처럼 사용하는 방식이다 !!
이 경우 아래의 두 그래프는 같은 feature vector를 가지게 된다.

1) Graphlet Features (Bag-of-graphlets)
Key Idea: graph에서 다른 graphlet의 개수를 세는 것
Graphlet의 정의는 node-level feature들과는 다르다 !!
두 가지 차이점이 있는데....
1) graphlets의 node들은 연결되어 있을 필요가 없다 (isolated node의 경우도 포함시킨다)
2) graphlet들은 root되어 있지 않다.
좀 더 예시를 들어서 이해해보자 !!
$\mathcal{G}k = (g_1,g_2, ...,g{n_k})$ 은 size k의 graphlet들의 list를 의미

graphlet count vector $f_G \in \mathbb{R}^{n_k}$
$(f_G)_i= num(g_i \subseteq G) for\ i=1,2,...,n_k$

두 개의 graph G와 G'가 주어질 때, graphlet kernel은 다음과 같이 연산된다.
$K(G,G')=f_G^Tf_{G'}$
문제
만약 G와 G'의 사이즈가 다를 때, value를 구할 수가 없다.
해결책은
각 feature vector를 normalize하는 것이다.

한계점은
Graphlet을 세는 것의 비용이 비싸다 !
size n인 Graph의 size k의 Graphlet의 개수를 세는 것은 $n^k$ 비용을 가지게 된다.
Subgraph Isomorphism Test는 NP-hard 문제이다.
graph의 node degree의 한계가 d일 때,
$O(nd^{k-1})$ algorithm은 size k의 모든 graphlet들의 개수를 센다.
2) Weisfeiler-Lehman Kernel (Bag-of-colors)
목표
효과적인 graph feature descriptor $\phi(G)$를 디자인하는 것
아이디어
node vocabulary를 반복적으로 풍부하게 하기 위해서 neighhood structure를 사용
- Bag of node degrees의 general version이다. 왜냐하면 node degree들은 one-hop 이웃 정보이기 때문이다.
- 이 알고리즘을 통해서 "Color Refinement"를 달성하는 것을 목표로 한다 !!
Color Refinement
nodes $V$의 set을 가진 graph $G$가 주어질 때,
초기 color인 $c^{(0)}(v)$를 각 node $v$마다 정해준다
반복적으로 node color들을 refine한다
$c^{(k+1)}(v)=HASH({c^{(k)}(v),{c^{(k)}(u)}_{u \in N(v)}}$,
HASH는 다른 input들에 다른 color들을 mapping해준다.
color refinement를 K step 진행한 뒤, $c^{(K)}(v)$는 K-hop neighborhood의 구조를 요약한다.
After color refinement,
WL Kernel은 주어진 color를 가진 node들의 개수를 센다.

WL kernel 값은 color count vector들의 Inner product로 연산할 수 있다.

WL kernel은 연산이 효과적이다.
각 step마다 color refinement에 대한 time complexity는 edge들의 개수에 linea하다.
kernel value를 연산할 때, graph에서만 나타난 color들에 대해서만 track해야 한다.
따라서, color의 개수는 대부분 모든 노드의 개수이다. color를 세는 것에는 linear-time이 걸린다.
⇒ 결론적으로, Time complexity는 edge의 개수에 linear한 것이다.
Today's Summary
Traditional ML Pipeline
Hand-crafted feature + ML model
Hand-crafted features for graph data
- Node-level : Node degree, clustering coefficient, centrality, graphlets
- Link-level : Distance-based feature, local/global neighborhood overlap
- Graph-level : Graphlet kernel, WL kernel
'GNN > CS224W Lecture note' 카테고리의 다른 글
| CS224W(2021) Lec 2-1 정리 (0) | 2021.11.17 |
|---|

