| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 소수 판정
- 그래프란
- paper review
- 백준
- CS224W
- 추천시스템 입문
- 글또8기
- numpy
- 질문 정리
- 에스토스테네스의 체
- graph
- 추천시스템
- zerodivide
- Graph Representation Learning
- #이코테2021
- 논문리뷰
- 유클리드 호제법
- nan값
- 이코테
- BruteForchSearch
- BruteForceSearch
- 데이콘 필사
- 알고리즘
- 강의정리
- allow_pickle
- 나동빈
- 파이썬 머신러닝 완벽가이드 공부
- 수학
- #나동빈
- 코테공부
- Today
- Total
꾸준히 써보는 공부 기록
CS224W(2021) Lec 2-1 정리 본문
1. Traditional Methods for ML in Graphs
Graph에서의 ML task들은 다음과 같다.
- Node-level prediction
- Link-level prediction
- Graph-level prediction
Traditional ML Pipeline의 경우에는
node / link / graph에 대한 feature들을 각각 design하게 된다. 그리고 모든 training data에 대해서 feature들을 포함하고 있다.

ML model을 training하는데는 Random Forest, SVM, Neural Network를 사용한다.
주어진 새로운 node / link / graph에 대해서, feature를 이용해서 prediction을 한다.
결론적으로 좋은 성능을 얻기 위해서 핵심이 되는 것은 graph에 대해서 효과적인 feature를 사용하는 것이다 !
Traditional ML pipeline에서는 hand-designed feature들을 사용한다. Traditional feature들을 3가지 level에서 보는데,
- Node-level prediction
- Link-level prediction
- Graph-level prediction
여기서는 undirected graph만 다룬다.
Graph에서의 ML Goal : object에 대한 prediction
Design choices
- Features : d차원 vectors
- Objects : node, edge, node의 집합, 전체 graph
- Object function : 해결하려는 task !!
Notations
$$G = (V, E)$$
이때 G는 그래프, V는 노드, E는 엣지를 의미한다. 그리고 학습하려는 function은 다음과 같이 표기한다.
$$f:V\rightarrow \mathbb{R}$$
그렇다면 function은 어떻게 학습할까??
2. Node-level Tasks and Features
Node-level Task → Node Classification

이 때 ML은 feature가 필요하다 !!
Node-level feature의 목표
network에서 하나의 node의 structure와 position을 특정 짓는 것이 목표이다.
Node feature의 종류
- Node Degree
- Node Centrality
- Clustering Coefficient
- Graphlets
이제 하나씩 살펴보자
1) Node Degree - Importance, Structure-based Node Features
Node v의 Degree $k_v$는 node가 가진 edge의 개수를 의미한다. 즉, node v의 neighbor node의 개수를 의미하게 된다. 이때 이웃 노드들에 대해서 같게 취급한다. (weight 값은 따로 고려하지 않는다.) 간단히 이웃 노드들의 개수를 카운트하는 것이다.
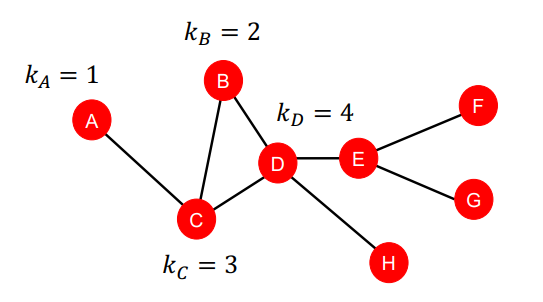
2) Node Centrality - Importance-based Node Features
graph에서의 node가 가지는 중요도를 고려하게 된다. Importance를 모델링하는 방법은 다양하게 있는데,
- Betweenness Centrality
- Closeness Centrality
- Eigenvector Centrality
- and many others....
Eigenvector Centrality
node v가 중요하다는 것의 근거는 노드 v가 중요한 이웃 노드들 $u \in N(v)$로 둘러싸여져 있다는 것이다.
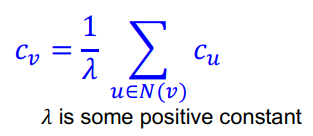
하지만 이렇게 모델링할 경우 recursive한 형태를 띄게 되는데, 이 부분의 해결 방법은 다음과 같다.
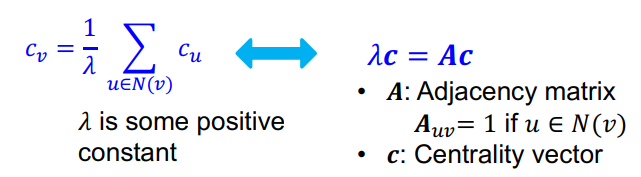
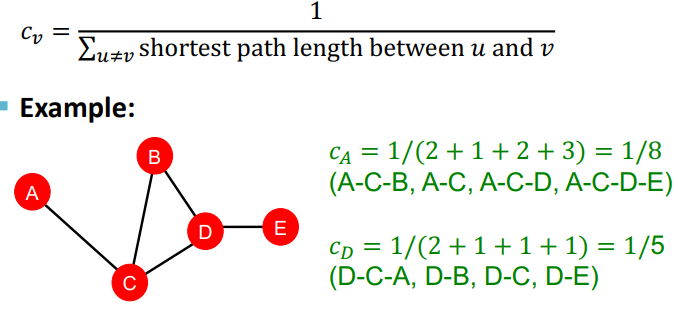
여기서 Centrality는 eigenvector로 볼 수 있다. 가장 큰 eigenvalue인 $\lambda_{max}$는 항상 positive하고 unique하다. (by Perron-Frobenius Theorem) Leading eigenvector인 $c_{max}$는 centrality 연산에 사용된다. 그래서 $c_v$는 어떻게 연산을 하는지에 대한 기준은 Betweenness와 Closeness로 나눠서 생각할 수 있다.
- Betweenness Centrality
다른 노드들 사이의 shortest path에 많이 나타날 수록 그 노드는 중요하다고 할 수 있다.
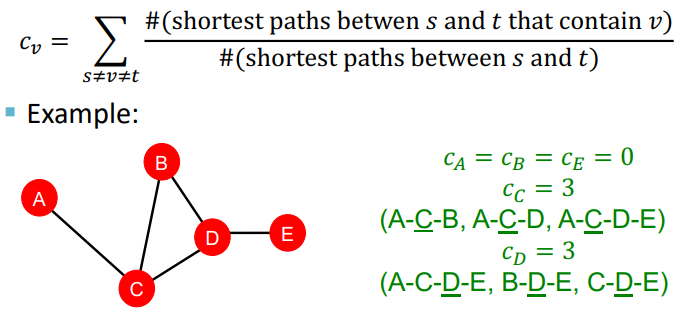
- Closeness Centrality
다른 노드들로 가는 shortest path의 길이가 짧을 수록 그 노드는 중요하다고 할 수 있다.
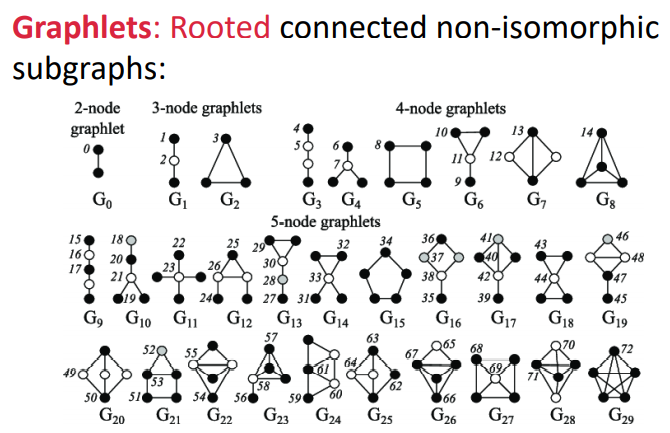
3) Graphlets : Structure-based Node features
Graphlet의 정의는 다음과 같다.
- Graphlet Degree Vector(GDV) : node들에 대한 Graphlet-base 특징
- Degree는 node에 연결된 edge들을 카운트한 것
- Clustering coefficient는 node에 연결된 triangle의 개수를 카운트한 것
- GDV는 node에 연결된 graphlet을 카운트한 것
예를 들면
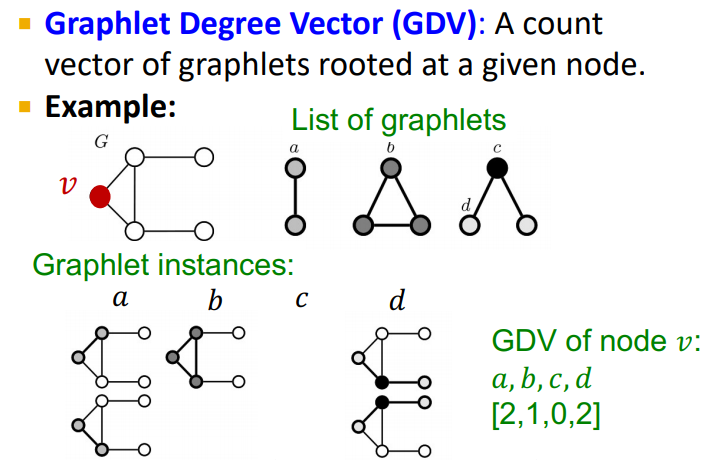
GDV는 노드의 "Local Network Topology"의 measure를 제공한다.
Summary
1. Importance-based Features
Graph에서 Node의 Importance를 찾아낸다.
- Node degree : 이웃 노드들의 개수를 카운트
- Node Centrality : 그래프에서 이웃 노드들의 importance를 modeling해서 고려
Importance-based feature의 경우, graph에서 영향력 있는 노드를 predict할 때 유용하다. 예를 들면, social network에서 celebrity user를 예측할 때 유용하다.
2. Structure-based Features
node 주위의 local neighborhood의 topological 특성을 찾아낸다.
- Node degree : 이웃 노드들의 개수를 카운트
- Clustering Coefficient : 이웃 노드들이 어떻게 연결되어 있는지
- Graphlet Degree Vector : 노드가 포함된 graphlet들을 카운트
Structure-based feature의 경우, graph에서 node가 특정한 역할을 하는지 예측할 때 유용하다. 예를 들면, PPI network에서 protein functionality를 예측할 때 유용하다.
사진 자료 출처 : CS224W : Machine Learning with Graphs
'GNN > CS224W Lecture note' 카테고리의 다른 글
| CS224W(2021) Lec 2-2 정리 (0) | 2021.12.28 |
|---|

